


Win Corduan
PAGE 4: PHI AND THE FIBONACCI SERIES
To go directly to Binet's Equation, click here.
Counting Rabbits
Well, I've indulged myself long enough, and I thank you for your patience. But now the time has come to start counting lagomorphs. I hope that in my preceding discussion I have made it clear that the so-called golden ratio number ϕ (phi), has a life of its own, apart from the Fibonacci series. If you have caught on to that point, we are now ready to talk about the Fibonacci numbers and how they are intertwined with phi. (If you still say that phi is derived from the Fibonaccis, you're probably only teasing me, or you didn't read the preceding posts on the topic.) Leonardo Bonacci (1170?-1250?) made a number of important contributions to math, the most significant of which is undoubtedly his promotion of the Indian/Arabic numerals in Europe, which made life a lot easier to anyone having to undertake any calculations. If you've heard of Leonardo at all, it was probably under his nickname, Fibonacci, and most likely in connection with the series of numbers that is designated after him. The series is embedded in a puzzle that Fibonacci posed to his reading audience (Livio, 96)): Please follow along with the picture as I walk us through the beginning of solving this puzzle. I might clarify, by the way, that we are counting the mature pairs only, just because that's how it's presented. The outcome would be no different if we counted immature pairs alongside the mature ones, except we would have only one numeral 1 at the outset, rather than two of them. (1) During the first month we have only the 1 original pair. 1 1 2 3 5 8 Each new number is created by taking the last two and adding them. So, let's continue this pattern until we reach the twelfth month, which will give us the answer to the specific puzzle that Fibonacci posed: 1 1 2 3 4 8 13 21 34 55 89 144 So, there will be 144 pairs of rabbits (288 individuals) living in the man's enclosure after a year. That doesn't sound too bad, but keep in mind that we are now entering a phase when the numbers will grow quite rapidly. Give it another three months, and the number will be 610 pairs, which is to say, of course, 1,210 grown rabbits. Then there will also be another 377 immature pairs (754 young rabbits), giving us a total of 1,964 rabbits hopping around, looking for lettuce and carrots. As fans of the Fibonacci series know, and as I have intimated already, there is a close relationship between the Fibonacci numbers and ϕ. Take a number in the series and divide it by the previous one, and you'll get some number that is in the vicinity of phi. So, let's look at two of such ratios. 1) The number of the tenth month (55), divided by that of the ninth (34): 55/34 = 1.617647059 ... 2) Since I brought up the fifteenth month, let's see what we get when we divide 610 by 377. The answer is 1.618037... Let us recall the approximate numerical value of phi: 1.618033988 ... . We can see that the longer we go on with the process, the closer we will get to phi. But there's something else that may not jump out at you immediately because of the many digits. Let us put these three numbers into numerical order, lower to higher:
A certain man put a pair of rabbits in a place surrounded on all sides by a wall. How many pairs of rabbits can be produced from that pair in a year if it is supposed that every month each pair begets a new pair which from the second month on becomes productive?

(2) In the second month the original pair will have produced one pair of offspring, which is not yet mature enough to produce any baby rabbits, so we are still holding at 1 mature pair.
(3) By the the time of the third month, the original pair will have given us another immature pair, and the earlier pair will now have matured, but not yet yielded any new rabbits. Thus the number we can put down for the third month for mature rabbits is 2.
(4) Come month 4, there is more offspring: one pair each from the original pair and the second generations pair. Also, the offspring from the newer pair will have matured. So the tally of mature rabbits for that month is 3.
(5) In the fifth month we get 5 mature rabbits, and each of the three that had matured in the previous month have contributed an as-yet immature pair.
(6) In the sixth month, the three previously immature ones will have matured and can get added to the previous five. Thus we have 8 mature pairs and five pairs that are only a month old--but probably can't wait until they are grown sufficiently to add to the pool.
(7) I trust that you can see the pattern that is developing. Month by month the collection of rabbits is increasing. The numbers of mature pairs that we have now for the first six months are:
| 10th number | 1.617647059 ... | < ϕ |
| Phi | 1.618033988 ... | = ϕ |
| 15th number | 1.618055556 ... | > ϕ |
The ratio of the 10th number to the 9th was below phi, whereas the estimate of the 15th to the 14th was a bit higher. This is one of the interesting aspects of the relationship between the Fibonacci series and ϕ: the different ratios of one number to its predecessor will always be an "approximation," though they get extremely close. But the direction of the error will alternate. The ratios with even numbered places in the series will be slightly lower than a more accurate rendering of ϕ, while the odd ones will exceed it just a little. Needless to say, as you have seen for yourself if you did the little exercise at the outset of this series, even with non-Fibonacci numbers the approximation gets very close, how much more within the Fibonacci series!
(We can't talk about the functions of a number without doing math. However, we're entering another section dealing with complex equations, so if you need to miss out on the excitement, please feel free to click here for a mysterious and instantaneous trip to the next page.)
Convergence of a Series
Let us recollect that theoretically, there need not have been a Fibonacci series in order for there to be a phi, since, as we have shown, the actual birth of phi occurred in geometry and number theory. The Fibonacci series can be described with an equation, in which Fn stands for the rank of a given Fibonacci number. What is the “nth” Fibonacci number?
(Fn = Fn-1 + Fn-2), where F1 and F2 = 1
e.g., the 9th Fibonacci number = the 8th Fibonacci number plus the 7th Fibonacci number
So, we can just remember the sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, … and fill in the slots.
34 = 21 + 13
John Derbyshire [Prime Obsession (Washington, DC: Joseph Henry Press, 2003)] presents us with a good illustration of convergence by contrasting it with its opposite result, called divergence. Most of this entry from this point on summarizes Derbyshire’s exposition on this point. “Divergence” means that the value of the series keeps growing and, thus, eventually could be said to be infinity (∞). He illustrates divergence by using the so-called harmonic series, which consists of the reciprocals of regular counting numbers (those that inhabit ℤ).

A close relative of the harmonic series does, in fact, converge. It’s as simple as re-creating the harmonic series, but using exponential powers of 2 as the denominators.

For a moment there you might think that, similar to the harmonic series, this one will also extend to infinity, but it doesn’t work out that way. To be sure, the number does keep growing; however, the rate of growth declines rapidly so that, as you go further along, the best you can get is near-identity with a finite number. Let’s see what happens when we add it up this far:

That’s pretty close to 2, and the further we go, the closer we will get, though we’ll never truly reach it. (Is anyone else reminded of the sizes of wrenches and sockets in an American-style set of tools?) We can say that the formula approaches 2, and that’s good enough for many purposes.

Similarly, the ongoing ratio of the Fibonacci series approaches phi.

and that, too, is good enough for many purposes.
One such purpose is to help us determine the “nth” Fibonacci number when it’s a long way up the chain, say the 20th, without having to memorize the entire set of Fibonacci numbers or go through the tedious method of generating the lengthy chain of 20 links. But the clock, my energy, and your patience all lead me to realize that I better save that adventure for the next entry.
*****
Most of this was written originally on Saturday evening, but needed some refinement and a lot of uploading of formulas, plus adding enough fun stuff to please my reading public. I hope you like the Staypuft Marshmallow Man® animation I concocted.
Well, let’s get back to the numbers.

There are several mathematical surprises connected to the Fibonacci series in its own right, apart from its involvement with ϕ. As intriguing as those things are, I need to refer you to Livio for details. If I don’t observe some limits, this series would still be going a year from now, and—who knows—even the spammers might be scared away by then. So I’m going to continue to focus on ϕ as much as I can, and talk some more specifically about the relationship between the Fibonacci series and ϕ.
There is a formula known as “Binet’s Equation,” named after Jacques Phillipe Binet (1786-1856), who was actually not the first person to discover it, but apparently created more interest in it than other famous mathematicians before him. Now, I’m going to trot out Binet’s equation, and you may just be horrified when you first see it. It looks like a huge monster, perhaps reminiscent of one such as the StayPuft Marshmallow ManŽ from “Ghost Busters®.” We’re going to describe Binet’s equation, and pare it down until it becomes one simple calculation. Then we’ll use it to find out what the 12th Fibonacci number is.
[Added on Monday: When I was working on this on Saturday night I had no guarantee that it would actually come out the way it should. To be more specific, I assumed that the formula was right, but I did not know if I was interpreting and using it correctly. If it didn’t work out, I had no one to ask, at least immediately, what I had done wrong. Thus, my emotional reaction at the end was totally authentic. I couldn’t believe that I had brought off both stages: understanding the formula (a good first step to clarifying it for my readers) and applying it in order to get the right answer. ]
If you just want the pay-off without the work, please click here.
Here goes. This is Binet’s Equation: Intimidated? You should be—but only until we’ve taken it apart and seen the simplicity that’s behind the apparent complexity. Seriously, I’m going to go extremely slowly in clarifying this equation and highlighting all steps. One of the nicest compliments I have ever received on my writing was with regard to my commentary on 1 and 2 Chronicles, when the editor at B&H told me: “Win, you have made Chronicles come alive.” I don’t know if it’s a comparable challenge, but I shall try to make Binet’s formula come alive as well. “Fn” stands for which Fibonacci number in the chain you wish to calculate, i.e. the “nth” number. This is totally of your own choosing. We’ll try to use the formula to figure out the 12th Fibonacci number, a number we can easily verify by just adding up the Fibonaccis. The expression “for n ϵ ℤ” reminds us that n has to be an integer. The Fibonacci numbers per se are not irrational, and are inhabitants of ℤ. The irrationality of phi and square root of 5 comes into play insofar as our answer may need rounding up or down to keep the solution within the ℤ circle as well. From here on out, we're going to dispense with that little tail. Wow! What are we going to do with that messy clutter highlighted in red? Actually, you may know already what we’re looking at here, once I let it stand by itself. It’s the positive root of our good old equation for ϕ: x2-x-1=0.
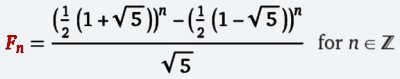


namely

So, we can substitute ϕ for that formula, and life is beginning to look a lot simpler already. We now know that, when the time comes for actual calculations, we can insert 1.61803 as the value of ϕ.

A similar thing is true for the next packet that I’ve highlighted in red.

This is the negative solution for phi’s equation, and you may or may not recall that it’s value is the same as the negative inverse conjugate of ϕ, but terminology aside and more importantly, you may remember that it amounts to -0.61803. Rather than writing “-1/ϕ”, which would mean that we're building up fractions again, I’ll use an expression that’s equivalent, but a little easier on the eyes, –ϕ-1.

Let’s not forget that, when we eventually subtract that negative number, we can substitute a “plus” sign for the two negatives—if we ever have to do so. The last thing I can point out before we actually install some numbers is that both ϕ and its negative reciprocal will be raised to the power of n.

Now we’re looking at the formula that we want to instantiate.

I know; I know. You’re probably still not buying into my claim of simplicity.
Okay, I have one more trick up my sleeve to try to persuade you, and it's a good one.
There’s a corner we may cut without doing ourselves any serious harm (just don’t run with the scissors, please). That whole –(–ϕ–1)n business is going to get extremely tiny, yea infinitesimal, so quickly that it can be pretty much treated as negligible for our practical purpose. I’m allowed to say that because this formula does have a practical purpose, namely to find a specific number in the Fibonacci series, and the Fibonacci numbers are all positive integers. (Alright, different definitions of “practical” perhaps.) If we give ourselves permission to leave off the negative part, we can actually calculate the “nth” Fibonacci number of the series with the simple formula: One multiplication (ϕ raised to the nth power) followed by one division, dividing the product by the square root of five.

We set out to find the 12th Fibonacci number, and now we’re at the point where we can put some numbers into that simplified formula. If our result comes out really skewed we’ll have to work a little harder. Let’s substitute 12 for n:

If you’re using a sophisticated math program, you can just plug in the symbols. I don’t expect that too many of us carry a value for ϕ12 in our heads, but Wolfram/Alpha has given me an answer of 321.987… for the top, the numerator. We can use a value of 2.236 for √5. So we can take that number and use it to divide Wolfram's calculation of ϕ12. The crucial moment is drawing nigh:

We do the division and get …
Let me tell you how nervous I am right now. As I said above, I have not done this before with all of the appropriate details. Before starting to write down anything formal, I gave it a rough once-over trying just to see if it might work, but now I’m really wondering. I’m sure you’re in suspense, too, about whether I worked it out so as to get a plausible result. Of course, it’s possible that it didn’t. I am fallible and prone to small mistakes that generate drastic changes in the outcome. That reminds me of a time when …

Okay, okay, I’ll stop dawdling. It’s taking me a bit to get past this approach/avoidance dilemma. Let’s take it to Wolfram then and have it do the last division for us. The expected answer was 144. Here is the result of applying the truncated form of Binet’s equation:
144.0015 …
I can’t believe it. I really, honestly did not expect anything nearly as close to 144. I’m stunned and almost emotional. This was a long and winding road. Thank you to those of you who stayed with me through the entire length of this entry. I know it was demanding. But isn’t that result a whole can of high-octane awesome-sauce‼
Back in my childhood days in Gymnasium, our math teacher, Frau Dr. von Borke, had us memorize the multiplication table for up to 20. Thus I realize that 144 is not only the 12th Fibonacci number, but also 122. I don't know whether there is any further mathematical significance to this fact, but we can see another piece of that beautiful mosaic of numbers. When God built numbers into the universe he created, he not only gave it regularity, but he suffused it with a beauty that we ignore to our own loss.
It’s too bad that it has become almost fashionable these days to promote yourself as someone who doesn’t get along with numbers, wearing that self-deprivation almost like a badge of machismo. Look at what you’re missing!
I wish all of my readers a day filled with beauty on many different levels.
Continue to Page 5
Return to Page 3

